Modeling Reaction-diffusion-mechanics
In the heart, electrical excitation propagates through diffusively coupled cardiac cells and subsequently results in contraction and force generation (excitation-contraction or electromechanic coupling). Mechanical forces on cardiac cells may in turn change electrophysiological properties of the tissue, e.g. action potential duration, or induce after-depolarizations resulting in premature beats. This so-called mechanoelectric feedback is therefore considered an important mechanism facilitating cardiac arrhythmias, however many of its details remain elusive. The objective of this project is to develop and analyze a generic model of cardiac electro-mechanics and to study mechanisms underlying the onset and perpetuation of cardiac arrhythmias. In order to answer this question, we are following Panfilov et al. and model cardiac tissue as a reaction-diffusion-mechanics system. This model consists of reaction-diffusion equations describing (simplified) cardiac electrophysiology, equations describing soft tissue mechanics, and the coupling between them. Finite deformation elasticity theory is required to describe the tissue dynamics, due to the significant change in cell length during contraction (typically 10-20%). Numerical simulations indicate that mechanical deformation may result in spiral wave drift and subsequent breakup [1]. Moreover, deformation may also result in spiral wave stabilization as shown in Fig. 1.
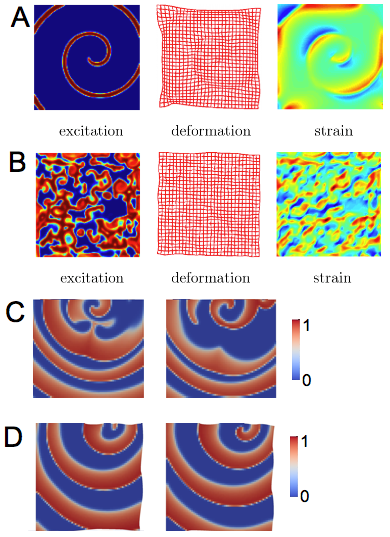
Figure 1 Reaction-Diffusion-Mechanics.
(A) Excitation, deformation and strain in a homogeneous, generic excitable and deformable two-dimensional medium. The image shows a stable spiral wave.
(B) Spiral wave breakup results in spatio-temporal chaos.
(C) Spiral wave in non-deforming medium shows wave breakup.
(D) Stable spiral wave in the deforming medium (same initial conditions and parameters as in panel (C)).
References
- R.H. Keldermann and M.P. Nash and A.V. Panfilov, Physica D 238, 1000-1007 (2009).