Unpinning Spiral Waves
While FF-AFP provides remarkable energy reduction compared to conventional therapeutic approaches, the underlying mechanisms remain largely elusive. Further optimization of LEAP requires identifying the mechanisms underlying the interaction of spiral waves and pacing-induced perturbations. One of the constituents of these complex dynamics is the interaction of pinned spirals – spiral waves that are anchored at anatomical obstacles such as fatty tissue, scars or blood vessels – with pulses of an electric field. The importance of pinned spirals lies in the fact that this kind of wave is resistant to other strategies of low-energy control such as antitachycardia pacing (ATP, see Fig. 1A). In a generic model of excitable media, we demonstrated that this significant limitation of ATP for unpinning spiral waves from obstacles could be overcome by LEAP [1,2,3]. The basic mechanism by which unpinning is achieved through LEAP is shown in Fig. 1B. A spiral wave anchored to a circular obstacle can be considered as a nonlinear phase oscillator with the phase (determined by the position of the spiral on the circle, see Fig. 1C) evolving uniformly in the unperturbed case. In this setting, we identified phase regimes of the rotating wave that result in different responses to a single electric field stimulus (see Fig. 1D) and investigated their dependence on the electric field strength and obstacle size [2]. In particular, we found that the response of the spiral wave to an FF-AFP perturbation can be characterized by a phase response map. Using this approach, mechanisms such as phase resetting can be observed, which are also known from other nonlinear oscillatory systems. These properties were used to predict the response of a pinned spiral wave to periodic pulse trains [4,5], a process that is probably taking place during the application of FF-AFP. Using an iterative map constructed from the phase response map, we were able to accurately predict unpinning success rates as a function of the pacing frequency and specifically to understand the occurrence of low success rates for certain frequency regimes (see Fig. 1E). These low success rates were due to a frequency locking mechanism between the spiral and the pacing, which is directly connected to periodic orbits of the iterated map.
Figure 1

(A) Unsuccessful unpinning of spiral wave pinned to circular heterogeneity by nearby periodic pacing site (P).
(B) Successful unpinning by FF-AFP. The nucleation of a new wave N by FF-AFP in the refractory tail of the original spiral leads to the formation of a free end F, which forms an unpinned spiral (new spiral core indicated by a circular white line), while the pinned end E of the pacing wave collides with the original spiral. Reproduced from [1].
(C) The net effect of an unsuccessful FF-AFP pulse is a phase shift, which depends on the phase !” of the spiral before the pulse. Thus, the reaction of the spiral to an unsuccessful pulse can be fully described by a so-called phase response curve.

(D) Schematic view of the spiral’s response to an FF-AFP pulse. A–E denote different FF-AFP regimes in phase space. A leads to no phase resetting, whereas B, D and E cause the phase to reset. C corresponds to successful unpinning. Reproduced from [2].
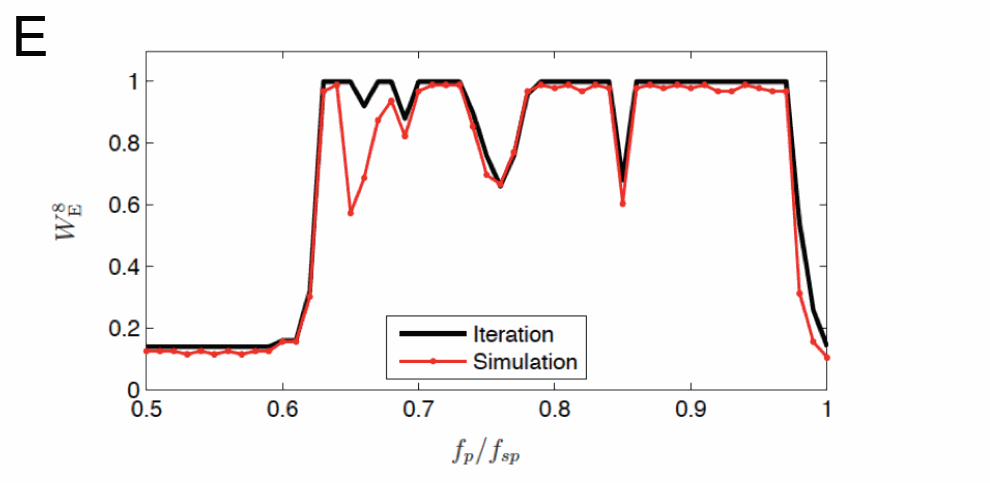
(E) Unpinning success rate WE8 for 8 FF-AFP pulses as a function of the pacing frequency fp normalized by the spiral’s rotation frequency fsp. Black line: Prediction from the single pulse phase response map measured as described in panel C. Fixed points and periodic orbits of the iterative map lead to WE8 < 1. Red line: Real success rate from direct numerical simulation.
References
- P. Bittihn et al., New J. Phys.10, 103012 (2008).
- P. Bittihn et al., Phil. Trans. R. Soc. A 368, 2221-2236 (2010).
- A. Pumir et al., Phys. Rev.E81, 010901(R) (2010).
- A.Behrend, P. Bittihn, S. Luther, Computing in Cardiology37, 345-348 (2010).
- A. Behrend, P. Bittihn, S. Luther, Biomed Tech 2010; 55 (Suppl. 1), DOI 10.1515/BMT.2010.339.